ESPECIFICACIONES DE LA RESPUESTA DE SEGUNDO ORDEN

Las características de la respuesta transitoria constituye uno de los factores más importante en el diseño de sistemas.

En muchos casos prácticos, las características deseadas de un sistema de control pueden darse en términos de las especifícaciones de la respuesta transitoria. Con frecuencia tales características de comportamiento se especifícan en términos de la respuesta transitoria a la entrada escalón unitario, puesto que éste es fácil de generar y es suficientemente eficaz.

Es importante estudiar la respuesta temporal del sistema dado que:

• Durante este régimen pueden aparecer, si es un sistema de tipo oscilatorio, valores muy elevados de las variables involucradas.
• Un régimen transitorio poco amortiguado no es aconsejable debido a que el desplazamiento del nivel esperdo toma valores instántaneos muy elevados.
• Si el transitorio es muy lento indica que el sistema toma demasiado tiempo en adaptarse a una entrada.

La respuesta transitoria de un sistema de control práctico a menudo muestra oscilaciones amortiguadas antes de alcanzar el estado estable, existen párametros de diseño basados en las especificaciones de dicha respuesta.

Un sistema muy estudiado cuya respuesta transitoria es característica de los sistema de control es un sistema de segundo orden:

La salida de un sistema de segundo orden ante un escalón unitario en el dominio laplaciano esta dada por: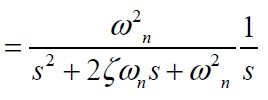

Al hallar la transformada inversa se obtiene la respuesta temporal: y(t)

Cuya curva de respuesta es la siguiente:

ESPECIFICACIONES:

tr = tiempo de subida:

tp = tiempo pico: es el tiempo requerido para que la respuesta alcance el primer pico de sobrepaso del valor final.

Mp = Sobrepaso o sobredisparo: es el valor del primer pico que tiene la respuesta.
Ts = tiempo de establecimiento. Es el tiempo requerido para que la respuesta del sistema mantenga oscilaciones dentro del rango del 2% del valor final.

ANÁLISIS DE LA RESPUESTA TEMPORAL DE UN SISTEMA

La respuesta en el tiempo de un sistema de control consta de dos partes: la respuesta transitoria y la respuesta en estado estable o también llamada en régimen permanente.
Se entiende por respuesta transitoria a la que va del estado inicial al estado final. Por respuesta permanente se entiende la forma en la cual la salida del sistema se comporta cuando t tiende a infinito.

Respuesta escalón de un sistema de primer orden:

Un sistema lineal de primer orden con una variable de entrada denotada x(t) (también puede ser r(t)) y una variable de salida denotada y(t) (o en otros casos c(t)) se modela matemáticamente con una ecuación que se puede escribir de la siguiente manera:

Siendo t la constante de tiempo del sistema y K la ganancia del sistema en estado estacionario:

Si el sistema se evalúa en este valor de t se puede conseguir que el sistema ha alcanzado el 63,2% del valor final.

Sea un sistema de primer orden, expresado mediante su función de transferencia:

La respuesta ante una entrada escalón unitario es la siguiente:

Como ejemplo se muestra la respuesta que correspondería al sistema G1 ante una entrada escalón unitario:

La constante de tiempo t del sistema es igual a 5 y como puede observarse en la gráfica representa el tiempo que tarda la respuesta en alcanzar el 63,2% del valor final 7*0,632=4,41.
El valor final está representado por:
y final = K x entrada



Respuesta escalón de un sistema de segundo orden:


Sistema de segundo orden:










Para una respuesta escalón unitario se obtiene la siguiente salida:

Enlaces que DEBEN revisar:

http://webdelprofesor.ula.ve/ingenieria/djean/index_archivos/Page502.htm
http://materias.fi.uba.ar/6722/respTransitoria.pdf
http://www.scribd.com/doc/7875167/Sistemas-de-segundo-orden

http://www.unet.edu.ve/~jlrodri/sist12.pdf

SEÑALES DE ENTRADA

En la práctica, la señal de entrada a un sistema dinámico no siempre se conoce por anticipado, inclusive puede ser de carácter aleatorio, sin embargo, se puede estudiar el comportamiento del sistema para entrada conocidas y así conocer su dinámica temporal.

Desde el punto de vista de diseño, es conveniente tener una base para comparar el funcionamiento de los diferentes sistemas. Esta base puede establecerse especificando señales de prueba partículares y despúes comparando las respuesta del sistema con estas señales de entrada. Muchos criterios de diseño se basan en tales señales: escalón, rampa, senoidales.

Señal Impulso

Señal Escalón

Señal Rampa

La señal de entrada que se seleccione para analizar las características dinámicas de un sistema puede determinarse por la forma de entrada que el sistema enfrente con mayor frecuencia durante su operación normal. Si se le somte a perturbaciones súbitas, una función escalón del tiempo puede ser una buena señal de prueba; para un sistema sujeto a entradas de choque puede ser mejor una señal impulso.
Una vez diseñado un sistema sobre la base de señales tipícas de prueba, su funcionamiento de respuesta a las entradas reales es generalmente satisfactorio.

FUNCIÓN DE TRANSFERENCIA

Análisis y Diseño de Sistemas Dinámicos

El análisis de sistemas constituye, es condiciones especificadas, la investigación del funcionamiento de un sistema cuyo modelo matemático se conoce.

El diseño de sistemas se refiere al proceso de encontrar un sistema que satisfaga una tarea específica.

El primer paso al analizar un sistema dinámico ( que evoluciona en el tiempo) consiste en obtener su modelo matemático.

En general los modelos matemáticos, constan de ecuaciones diferenciales. Dado que se trabajará con ecuaciones diferenciales lineales, invariantes en el tiempo puede usarse el método de la Transformada de Laplace para su resolución. Su ventaja principal es que la diferenciación de la función del tiempo corresponde a la multiplicación de la transformada por una variable compleja s, y así las ecuaciones diferenciales en el tiempo se hacen ecuaciones algebraicas en s. La solución de la ecuación diferencial puede, por tanto, encontrarse mediante el uso de una tabla de transformada de Laplace o por la técnica de expansión en fracciones parciales. Otra ventaja del método, es que al resolver la ecuación diferencial, las condiciones iniciales quedan automáticamente incluidas.

En el análisis de sistemas de control no se hará énfasis en el rigor matemático de la transformada de Laplace sino en los métodos de aplicación asociados con el análisis y el diseño de sistemas lineales.

En la teoría de los sistemas las funciones llamadas “funciones de transferencia” se usan frecuentemente para caracterizar las relaciones de entrada y salida de sistemas de ecuaciones diferenciales lineales, invariantes en el tiempo.

La Función de Transferencia de un sistema de ecuaciones diferenciales lineales, invariantes en el tiempo, se define como la relación de la transformada de Laplace de la salida (función de respuesta) y la transformada de Laplace de la entrada (función impulsora) bajo la suposición que todas las condiciones iniciales sean cero.

Consideraciones:

• La función de transferencia de un sistema es un modelo matemático que implica un método operacional de expresar la ecuación diferencial que relaciona la variable de salida con la variable de entrada.


• La función de transferencia es una propiedad del sistema en sí mismo, independiente de la magnitud y naturaleza de la función de entrada o excitación.


• La función de transferencia incluye las unidades necesarias para relacionar la entrada con la salida; sin embargo. No proporciona información alguna concerniente a la estructura física del sistema. (Las funciones de transferencia de muchos sistemas físicamente diferente pueden ser iguales)


• Si la función de transferencia de un sistema se conoce, puede estudiarse la salida, o respuesta para varias formas de entrada teniendo presente la comprensión de la naturaleza del sistema.


• Sino se conoce la función de transferencia de un sistema, ésta puede establecerse experimentalmente introduciendo entradas conocidas y estudiando la salida del sistema. Una vez establecida, una función de transferencia da una descripción completa de las características dinámicas del sistema, sin recurrir a su descripción física.