Las especificaciones dinámicas en el dominio del tiempo más empleadas son:
Sobredisparo:

Tiempo de asentamiento

Tiempo pico y error en régimen permanente.
Recordando que la ecuación de los polos dominantes, resultantes de una dinámica de segundo orden, esta dada por:

Puede observarse de las ecuaciones anteriores que, el tiempo de establecimiento depende únicamente de la parte real de los polos y la sobreoscilación depende únicamente del amortiguamiento.
Lo habitual es que se fijen los polos de forma que la sobreoscilación del sistema en bucle cerrado sea entre el 4 y el 10%, es decir, que la parte imaginaria tenga un valor similar o algo mayor que la parte real.
Así pues, se determinan las características deseadas de la respuesta y a partir de ellas se calcula el par de polos:
*.-Se fija el tiempo de establecimiento deseado. De aquí se obtiene la parte real de los polos necesarios.

*.-Se fija la sobreoscilación deseada (puede ser un rango, por ejemplo entre el 5 y el 10%). De aquí se obtiene el amortiguamiento y de ahí la parte imaginaria necesaria.
Punto 2.
Para elegir el tipo de controlador (P, PD, PI ó PID) hay que tener en cuenta lo siguiente:
2.1 El término integral (PI ó PID) es necesario si se quiere garantizar que el error en régimen permanente (cuando pase mucho tiempo) sea nulo, es decir, si se quiere que la salida del proceso alcance exactamente el valor de la referencia.
2.2 La respuesta más rápida se consigue con el controlador PD (sin término integral), después con el PID, después con el P, y la más lenta con el controlador PI.
2.3 El término derivativo requiere que la señal del sensor no sea demasiado ruidosa. Si la señal del sensor es muy ruidosa el término derivativo puede dar problemas, por lo que puede ser conveniente un controlador P ó PI.
Lo más habitual es elegir el controlador PID completo, pues suele ser un buen compromiso entre rapidez de respuesta y error.
Punto 3.
Para fijar los ceros del controlador la estrategia depende del tipo de controlador. Si el controlador es PD ó PI, únicamente se tiene un cero, por lo que éste se fijará para que el lugar de las raíces pase por el par de polos deseados (solo habrá una solución en general).
Si el controlador es PID, entonces hay dos ceros, y existen infinitas soluciones. Lo más habitual es forzar a que los dos ceros sean iguales, con lo que únicamente queda una incógnita, que se fija igual que en el caso anterior.
También se puede fijar uno de ellos de forma arbitraria (por ejemplo de un polo del proceso) y elegir el otro para que el lugar de las Raíces pase por el par de polos.

Punto 4
Otra forma muy utilizada para hallar lo ceros y polos, y en consecuencia los parámetros del controlador es despejar de la ecuación característica la función de transferencia del controlador.
La función caracteristica de un sistema de lazo cerrado es:

Despejando la función de transferencia del regulador o controlador se tiene:
Para calcular el controlador se sustituye la variable s por el polo dominante previamente fijado y que satisfacen la ecuación característica.

Con esta ultima expresión se obtiene el regulador en su parte real y parte imaginaria. A partir de la expresión de las mismas se detrmina la ganancia y los prámetros del controlador.
Punto 5:
Por utlimo se verifica que cumpla las especificaciones y el error en regimen permanente.




 Diseñe un controlador proporcional derivativo de tal forma que el factor de amortiguamiento sea 0.7 y la frecuencia natural no amortiguada sea 0.5 rad/seg.
Diseñe un controlador proporcional derivativo de tal forma que el factor de amortiguamiento sea 0.7 y la frecuencia natural no amortiguada sea 0.5 rad/seg.





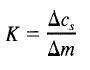
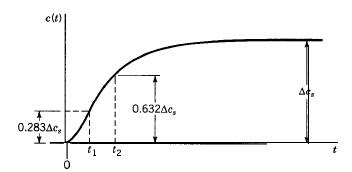


 Tiempo de asentamiento
Tiempo de asentamiento Tiempo pico y error en régimen permanente.
Tiempo pico y error en régimen permanente. Puede observarse de las ecuaciones anteriores que, el tiempo de establecimiento depende únicamente de la parte real de los polos y la sobreoscilación depende únicamente del amortiguamiento.
Puede observarse de las ecuaciones anteriores que, el tiempo de establecimiento depende únicamente de la parte real de los polos y la sobreoscilación depende únicamente del amortiguamiento.




 Con esta ultima expresión se obtiene el regulador en su parte real y parte imaginaria. A partir de la expresión de las mismas se detrmina la ganancia y los prámetros del controlador.
Con esta ultima expresión se obtiene el regulador en su parte real y parte imaginaria. A partir de la expresión de las mismas se detrmina la ganancia y los prámetros del controlador.