miércoles, 25 de noviembre de 2009
CUESTIONARIO
Sistema, Sistema de Control, Sistema Dinámico, Planta, Proceso, Variables de entrada, Variables de Control, Variables de Salida, Perturbaciones
2.- En que se basa el principio del control realimentado.
3.- Cuales son los objetivos del control realimentado y que ventajas ofrece.
4.- Cual es la función del controlador. Que criterios se deben tomar en cuenta para su diseño?
5.- Explique las diferencias entre un sistema a lazo abierto y un sistema a lazo cerrado.
6.- Describa el efecto que tiene cada acción del controlador (P, I, D) sobre la salida de un sistema.
lunes, 16 de noviembre de 2009
ACCIÓN DEL PID
 mientras la función de transferencia es:
mientras la función de transferencia es: Parámetros característicos:
Parámetros característicos: · Tiempo derivativo: Td.
· Tiempo integral Ti.
En general si se aumenta el valor de Kp: mejora la rapidez, disminuye el error, y aumenta la sobreoscilación.
- permite anular el error en régimen permanente
- implica un retraso: tiende a inestabilizar
- a menor Ti más rápido se anula el error, pero el sistema tiende a ser más inestable
- efecto anticipativo estabilizador (es una predicción del valor futuro del error)
- tiende a reducir la sobreoscilación
· El regulador PID introduce un polo en s=0 y dos ceros:

Igualando coeficiente a coeficiente del polinomio del numerador se obtienen las relaciones:

· El regulador PD introduce un cero:

· El regulador PI introduce un cero y un polo s=0:
 La estrategia de diseño del controlador consistirá en definir los ceros (zd y zi) y la constante KR para lograr que el sistema en bucle cerrado tenga los polos adecuados. Una vez calculados estos parámetros, se utilizarán las relaciones anteriores para obtener los parámetros finales del controlador: Kp, Td y Ti.
La estrategia de diseño del controlador consistirá en definir los ceros (zd y zi) y la constante KR para lograr que el sistema en bucle cerrado tenga los polos adecuados. Una vez calculados estos parámetros, se utilizarán las relaciones anteriores para obtener los parámetros finales del controlador: Kp, Td y Ti. martes, 10 de noviembre de 2009
EJEMPLO DE UN PID


PID COMO ESTRATEGIA DE CONTROL
El controlador PID (Proporcional, Integral y Derivativo) es un controlador realime ntado cuyo propósito es hacer que el error en estado estacionario, entre la señal de referencia y la señal de salida de la planta, sea cero de manera asintótica en el tiempo, lo que se logra mediante el uso de la acción integral. Además el controlador tiene la capacidad de anticipar el futuro a través de la acción derivativa que tiene un efecto predictivo sobre la salida del proceso.
ntado cuyo propósito es hacer que el error en estado estacionario, entre la señal de referencia y la señal de salida de la planta, sea cero de manera asintótica en el tiempo, lo que se logra mediante el uso de la acción integral. Además el controlador tiene la capacidad de anticipar el futuro a través de la acción derivativa que tiene un efecto predictivo sobre la salida del proceso.
Los controladores PID son suficientes para resolver el problema de control de muchas aplicaciones en la industria, particularmente cuando la dinámica del proceso lo permite (en general procesos que pueden ser descritos por dinámicas de primer y segundo orden), y los requerimientos de desempeño son modestos (generalmente limitados a especificaciones del comportamiento del error en estado estacionario y una rápida respuesta a cambios en la señal de referencia).
Su uso extensivo en la industria es tal que el 95% de los lazos de control que existen en las aplicaciones industriales son del tipo PID, de los cuales la mayoría son controladores PI, lo que muestra la preferencia del usuario en el uso de leyes de control muy simples.
El microprocesador ha tenido una influencia dramática sobre el desarrollo del controlador PID; ha permitido brindar nuevas oportunidades para implementar funciones adicionales como el ajuste automático de parámetros y los cambios de modos de control.
Los algoritmos actuales se combinan con funciones lógicas y secuenciales y una serie de mecanismos y funciones adicionales para adecuarse a los requerimientos de los modernos sistemas de control y automatización industrial, lo que da lugar a dispositivos especializados para el control de temperatura, velocidad, distribución de energía, transporte, máquinas-herramientas, reacción química, fermentación, entre otros.
lunes, 9 de noviembre de 2009
PRINCIPIOS DE DISEÑO DE CONTROLADORES POR REALIMENTACIÓN
a) Mantener Estabilidad.
b) Minimizar el error en estado estacionario.
c) Dar cierta forma a la respuesta dinámica.
El requisito de estabilidad a lazo cerrado se explica por si mismo. El error alcanzado por el controlador en estado estacionario debería ser tan pequeño como sea posible. El requisito del tipo o naturaleza de respuesta dinámica se puede desglosar en la satisfacción de los siguientes puntos:
Tiempo mínimo de elevación (tr)
Tiempo mínimo de amortiguamiento (ts)
Sobredisparo mínimo (a1)

CLASIFICACIÓN DE LOS SISTEMAS DE CONTROL
Un sistema de control de lazo abierto es aquel en el cual la acción de control es independiente de la salida. Los sistemas de control a lazo abierto tienen dos rasgos sobresalientes :
a) La habilidad que éstos tienen para ejecutar una acción con exactitud está determinada por su calibración . Calibrar significa establecer o restablecer una relación entre la entrada y la salida con el fin de obtener del sistema la exactitud deseada .
b) Estos sistemas no tienen el problema de la inestabilidad, que presentan los de lazo cerrado .

La principal desventaja es que las perturbaciones no pueden ser corregidas, por tanto al no haber medición hay incertidumbre y no hay posibilidad de corrección.
Un sistema de control de lazo cerrado es aquel en el que la acción de control es en cierto modo dependiente de la salida. Los sistemas de control de lazo cerrado se llaman comúnmente sistemas de control por realimentación.
El lazo de control realimentado simple sirve para ilustrar los cuatro elementos principales de cualquier lazo de control:
Los procesos industriales no son estáticos, por el contrario son muy dinámicos, cambian continuamente debido a los muchos tipos de perturbaciones y precisamente por eso se necesita que los sistemas de control vigilen continua y automáticamente las variaciones que se deben controlar.
El objetivo del sistema de control automático de procesos es utilizar la variable manipulada para mantener la variable controlada en el punto de control a pesar de las perturbaciones.CONTROL AUTOMÁTICO
El control automático de procesos se usa fundamentalmente porque reduce el costo de los procesos industriales, lo que compensa la inversión en equipo de control. Además hay muchas ganancias intangibles, como por ejemplo la eliminación de mano de obra pasiva, la cual provoca una demanda equivalente de trabajo especializado. La eliminación de errores es otra contribución positiva del uso del control automático .
El principio del control automático o sea el empleo de una realimentación o medición para accionar un mecanismo de control, es muy simple . El mismo principio del control automático se usa en diversos campos, como control de procesos químicos y del petróleo , control de hornos en la fabricación del acero, control de máquinas herramientas, y en el control y trayectoria de un proyectil .
El control automático es el mantenimiento de un valor deseado
dentro de una cantidad o condición, midiendo el valor existente, comparándolo
con el valor deseado, y utilizando la diferencia para proceder a reducirla. En
consecuencia, el control automático exige un lazo cerrado de acción y reacción
que funcione sin intervención humana .
EL PRINCIPIO DE REALIMENTACIÓN
Incrementar la variable manipulada cuando la variable del proceso sea más pequeña que la referencia y disminuirla cuando ésta sea más grande.
Este tipo de realimentación se llama “realimentación negativa” debido a que la variable manipulada se mueve en la dirección opuesta a la variable del proceso. El principio puede ser ilustrado por el diagrama de bloques que se muestra en la Fig. 1.

La realimentación es la propiedad de un sistema de lazo cerrado que permite que la salida ( o cualquier otra variable controlada del sistema ) sea comparada con la entrada al sistema ( o con una entrada a cualquier componente interno del mismo con un subsistema ) de manera tal que se pueda establecer una acción de control apropiada como función de la diferencia entre la entrada y la salida. Más generalmente se dice que existe realimentación en un sistema cuando existe una secuencia cerrada de relaciones de causa y efecto ente las variables del sistema.
Características de la realimentación.
Los rasgos mas importante que la presencia de realimentación imparte a un sistema son:
a) Aumento de la exactitud. Por ejemplo, la habilidad para reproducir la entrada fielmente.
b) Reducción de la sensibilidad de la salida, correspondiente a una determinada entrada, ante variaciones en las características del sistema.
c) Efectos reducidos de la no linealidad y de la distorsión.
d) Aumento del intervalo de frecuencias ( de la entrada ) en el cual el sistema responde satisfactoriamente ( aumento del ancho de banda )
e) Tendencia a la oscilación o a la inestabilidad .
viernes, 9 de octubre de 2009
ESPECIFICACIONES DE LA RESPUESTA DE SEGUNDO ORDEN
- Durante este régimen pueden aparecer, si es un sistema de tipo oscilatorio, valores muy elevados de las variables involucradas.
- Un régimen transitorio poco amortiguado no es aconsejable debido a que el desplazamiento del nivel esperdo toma valores instántaneos muy elevados.
- Si el transitorio es muy lento indica que el sistema toma demasiado tiempo en adaptarse a una entrada.
La respuesta transitoria de un sistema de control práctico a menudo muestra oscilaciones amortiguadas antes de alcanzar el estado estable, existen párametros de diseño basados en las especificaciones de dicha respuesta.
Un sistema muy estudiado cuya respuesta transitoria es característica de los sistema de control es un sistema de segundo orden:

La salida de un sistema de segundo orden ante un escalón unitario en el dominio laplaciano esta dada por: 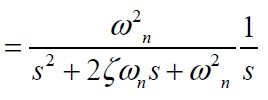
Al hallar la transformada inversa se obtiene la respuesta temporal: y(t)

Cuya curva de respuesta es la siguiente:

ESPECIFICACIONES:
tr = tiempo de subida:

 tp = tiempo pico: es el tiempo requerido para que la respuesta alcance el primer pico de sobrepaso del valor final.
tp = tiempo pico: es el tiempo requerido para que la respuesta alcance el primer pico de sobrepaso del valor final. Mp = Sobrepaso o sobredisparo: es el valor del primer pico que tiene la respuesta.
Mp = Sobrepaso o sobredisparo: es el valor del primer pico que tiene la respuesta. Ts = tiempo de establecimiento. Es el tiempo requerido para que la respuesta del sistema mantenga oscilaciones dentro del rango del 2% del valor final.
Ts = tiempo de establecimiento. Es el tiempo requerido para que la respuesta del sistema mantenga oscilaciones dentro del rango del 2% del valor final.
domingo, 4 de octubre de 2009
ANÁLISIS DE LA RESPUESTA TEMPORAL DE UN SISTEMA
Se entiende por respuesta transitoria a la que va del estado inicial al estado final. Por respuesta permanente se entiende la forma en la cual la salida del sistema se comporta cuando t tiende a infinito.
Un sistema lineal de primer orden con una variable de entrada denotada x(t) (también puede ser r(t)) y una variable de salida denotada y(t) (o en otros casos c(t)) se modela matemáticamente con una ecuación que se puede escribir de la siguiente manera:

Siendo t la constante de tiempo del sistema y K la ganancia del sistema en estado estacionario:

Si el sistema se evalúa en este valor de t se puede conseguir que el sistema ha alcanzado el 63,2% del valor final.
Sea un sistema de primer orden, expresado mediante su función de transferencia:
 La respuesta ante una entrada escalón unitario es la siguiente:
La respuesta ante una entrada escalón unitario es la siguiente:
Como ejemplo se muestra la respuesta que correspondería al sistema G1 ante una entrada escalón unitario:


La constante de tiempo t del sistema es igual a 5 y como puede observarse en la gráfica representa el tiempo que tarda la respuesta en alcanzar el 63,2% del valor final 7*0,632=4,41.
El valor final está representado por:
y final = K x entrada
Respuesta escalón de un sistema de segundo orden:
Sistema de segundo orden:



Para una respuesta escalón unitario se obtiene la siguiente salida:

Enlaces que DEBEN revisar:
http://webdelprofesor.ula.ve/ingenieria/djean/index_archivos/Page502.htm
http://materias.fi.uba.ar/6722/respTransitoria.pdf
http://www.scribd.com/doc/7875167/Sistemas-de-segundo-orden
SEÑALES DE ENTRADA
Desde el punto de vista de diseño, es conveniente tener una base para comparar el funcionamiento de los diferentes sistemas. Esta base puede establecerse especificando señales de prueba partículares y despúes comparando las respuesta del sistema con estas señales de entrada. Muchos criterios de diseño se basan en tales señales: escalón, rampa, senoidales.

Señal Impulso


Señal Rampa
La señal de entrada que se seleccione para analizar las características dinámicas de un sistema puede determinarse por la forma de entrada que el sistema enfrente con mayor frecuencia durante su operación normal. Si se le somte a perturbaciones súbitas, una función escalón del tiempo puede ser una buena señal de prueba; para un sistema sujeto a entradas de choque puede ser mejor una señal impulso.
Una vez diseñado un sistema sobre la base de señales tipícas de prueba, su funcionamiento de respuesta a las entradas reales es generalmente satisfactorio.
FUNCIÓN DE TRANSFERENCIA
El análisis de sistemas constituye, es condiciones especificadas, la investigación del funcionamiento de un sistema cuyo modelo matemático se conoce.
El diseño de sistemas se refiere al proceso de encontrar un sistema que satisfaga una tarea específica.
El primer paso al analizar un sistema dinámico ( que evoluciona en el tiempo) consiste en obtener su modelo matemático.
En general los modelos matemáticos, constan de ecuaciones diferenciales. Dado que se trabajará con ecuaciones diferenciales lineales, invariantes en el tiempo puede usarse el método de la Transformada de Laplace para su resolución. Su ventaja principal es que la diferenciación de la función del tiempo corresponde a la multiplicación de la transformada por una variable compleja s, y así las ecuaciones diferenciales en el tiempo se hacen ecuaciones algebraicas en s. La solución de la ecuación diferencial puede, por tanto, encontrarse mediante el uso de una tabla de transformada de Laplace o por la técnica de expansión en fracciones parciales. Otra ventaja del método, es que al resolver la ecuación diferencial, las condiciones iniciales quedan automáticamente incluidas.
En el análisis de sistemas de control no se hará énfasis en el rigor matemático de la transformada de Laplace sino en los métodos de aplicación asociados con el análisis y el diseño de sistemas lineales.

En la teoría de los sistemas las funciones llamadas “funciones de transferencia” se usan frecuentemente para caracterizar las relaciones de entrada y salida de sistemas de ecuaciones diferenciales lineales, invariantes en el tiempo.
La Función de Transferencia de un sistema de ecuaciones diferenciales lineales, invariantes en el tiempo, se define como la relación de la transformada de Laplace de la salida (función de respuesta) y la transformada de Laplace de la entrada (función impulsora) bajo la suposición que todas las condiciones iniciales sean cero.
Consideraciones:
- La función de transferencia de un sistema es un modelo matemático que implica un método operacional de expresar la ecuación diferencial que relaciona la variable de salida con la variable de entrada.
- La función de transferencia es una propiedad del sistema en sí mismo, independiente de la magnitud y naturaleza de la función de entrada o excitación.
- La función de transferencia incluye las unidades necesarias para relacionar la entrada con la salida; sin embargo. No proporciona información alguna concerniente a la estructura física del sistema. (Las funciones de transferencia de muchos sistemas físicamente diferente pueden ser iguales)
- Si la función de transferencia de un sistema se conoce, puede estudiarse la salida, o respuesta para varias formas de entrada teniendo presente la comprensión de la naturaleza del sistema.
- Sino se conoce la función de transferencia de un sistema, ésta puede establecerse experimentalmente introduciendo entradas conocidas y estudiando la salida del sistema. Una vez establecida, una función de transferencia da una descripción completa de las características dinámicas del sistema, sin recurrir a su descripción física.


domingo, 27 de septiembre de 2009
INTRODUCCIÓN
Hoy día, conocer los fundamentos de los sistemas de control y de la automatización resulta muy útil por cuanto culaquier ingeniero, independientemente de su titulación y de las tareas que tenga encomendada en relación con su trabajo en muy probable que tenga contacto con estos temas.
Algunos conceptos relacionados con la terminología a utilizar:
Sistema: consiste en un conjunto de elementos que actúan coordinadamente para realizar un onjetivo determinado.
Sistema de Control: Se puede definir como un conjunto de elementos que interactúan para conseguir que la salida de un proceso se comporte tal y como se desea, mediante una acción de control.
Planta: Es el elemento físico que se desea controlar. Planta puede ser: un motor, un horno, un tanque de agua, un sistema de disparo, un sistema de navegación, un tanque de conbustible, etc.
Proceso: Consiste en un conjunto de elementos que actúan coordinadamente para realizar un objetivo determinado. El procesamiento se realiza sobre una planta o una máquina, que son el conjunto de componentes y piezas que van a tener un determinado objetivo.
 las acciones pertinentes, las variables importantes del proceso, es decir, aquellas que se relacionan con su seguridad, la calidad del producto y los índices de producción, no cumplirán con las condiciones de diseño para lo cual fue pensado.
las acciones pertinentes, las variables importantes del proceso, es decir, aquellas que se relacionan con su seguridad, la calidad del producto y los índices de producción, no cumplirán con las condiciones de diseño para lo cual fue pensado.